Simulating solids and phase transitions
WARNING: FORTRAN IS A PAIN
For the Computational physics course project I took a bunch of particles (16) and threw them into a small box (actually its a 4x4 space which is repeated through periodic boundary conditions) and said that they could interact via the Lennard Jones Potential (i.e when particles are close together they feel strong electrostatic repulsion and when they are far away they feel attraction due to VanderWalls force. I saw the particles arrange them selves into regular triangular grids and then break away as I heated the system.
Report
For the Computational physics course project I took a bunch of particles (16) and threw them into a small box (actually its a 4x4 space which is repeated through periodic boundary conditions) and said that they could interact via the Lennard Jones Potential (i.e when particles are close together they feel strong electrostatic repulsion and when they are far away they feel attraction due to VanderWalls force. I saw the particles arrange them selves into regular triangular grids and then break away as I heated the system.
Report
Hamiltonian Chaos and Statistical Mechanics

Invariant Tori
The foundation stone of all the statistical ensembles is the Ergodic Hypothesis, where one assumes that if a system is left for long enough it will go through all phase states possible. We first assume that the molecules are interacting i.e. there are non-linear cross terms in the Hamiltonian and due to these terms the particles can interact and share energy reaching equipartition as predicted
Chaos was assumed to be a sufficient condition to believe in the Ergodic Hypothesis. The Fermi Pasta Ulam Experiment showed otherwise. This course project for my Statistical Mechanics course, based on a partial review of "Chaos and Coarse Graining in Statistical Mechanics" by Patrizia Castiglione, repeated their simulations and reviewed the basis of the Ergodic Hypothesis.
Surprisingly, some chaotic systems do not reach equipartition and some states regain their energies even after loosing them to other states due to some some leftover invariant tori. I also presented these ideas at the departmental Brown Bag!
[1] http://www.pip.uni-bremen.de/index.php?option=com_content&task=view&id=56&Itemid=39
Report
Brown Bag Presentation
Chaos was assumed to be a sufficient condition to believe in the Ergodic Hypothesis. The Fermi Pasta Ulam Experiment showed otherwise. This course project for my Statistical Mechanics course, based on a partial review of "Chaos and Coarse Graining in Statistical Mechanics" by Patrizia Castiglione, repeated their simulations and reviewed the basis of the Ergodic Hypothesis.
Surprisingly, some chaotic systems do not reach equipartition and some states regain their energies even after loosing them to other states due to some some leftover invariant tori. I also presented these ideas at the departmental Brown Bag!
[1] http://www.pip.uni-bremen.de/index.php?option=com_content&task=view&id=56&Itemid=39
Report
Brown Bag Presentation
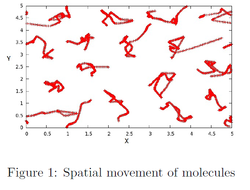
Spatio Temporal Characteristics of a Plankton prey predator system

Zooplankton
I learnt in my Non-Linear Dynamics course. All the attractors, repellers and limit cycles that I learnt about in my Non-Linear Dynamics course weren't very real as they were still based on the activities of a single point that traveled through phase space as. As a course project I ventured into the realm of spatio-temporal chaos. A place where limit cycles were born and died in the middle of the system and oscillating systems became chaotic without warning. This project reproduced the first few sections of the results discussed in the paper titled "Spatiotemporal Complexity of Plankton and Fish Dynamics" by Medvinsky et. al.
This still just looks at a one dimensional case (for x going from 0 - 900) but plankton of course live in 3. If homogeneous initial conditions are applied the system just oscillates as a normal prey predator system. However if for example the phytoplankton population varies with x even just slightly the system spirals into chaos after some time. Diffusion is allowed and the boundaries follow Neuman zero flux conditions. Interestingly the space average populations of the plankton is more stable in the chaotic regime.
Report
M File
This still just looks at a one dimensional case (for x going from 0 - 900) but plankton of course live in 3. If homogeneous initial conditions are applied the system just oscillates as a normal prey predator system. However if for example the phytoplankton population varies with x even just slightly the system spirals into chaos after some time. Diffusion is allowed and the boundaries follow Neuman zero flux conditions. Interestingly the space average populations of the plankton is more stable in the chaotic regime.
Report
M File
Summer Research - HER2 proteins and Cancer

In the Sophomore summer I participated in the Mathematics Undergraduate Research experience. Working with Dr. Adnan Khan we reproduced results of A Mathematical Model for the E
ffects of HER2 Over expression on Cell Proliferation in Breast Cancer by A. Eladdadi. We further non-dimensionalized the system and repeated the simulations. The session finished in a poster session where we came a close fourth.
Poster Last draft
Poster Last draft
Making EEGs
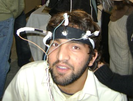
As a new students in a new university our aims were high. For our introductory electronics lab course Shabbir and I tried to make a super low cost EEG headgear. It was simple, three electrodes made of cotton dipped in Gatorade coupled with the required filtering electronics. It came third as the 'most ambitious student project.'
